Este es el primero de una serie de artículos cuyo objetivo final es entender el Valor en riesgo por Montecarlo (VaR using Monte Carlo Simulation). El valor en riesgo es un estadístico muy potente que cuantifica el alcance de las posibles pérdidas de una empresa, cartera o posición durante un periodo de tiempo específico.
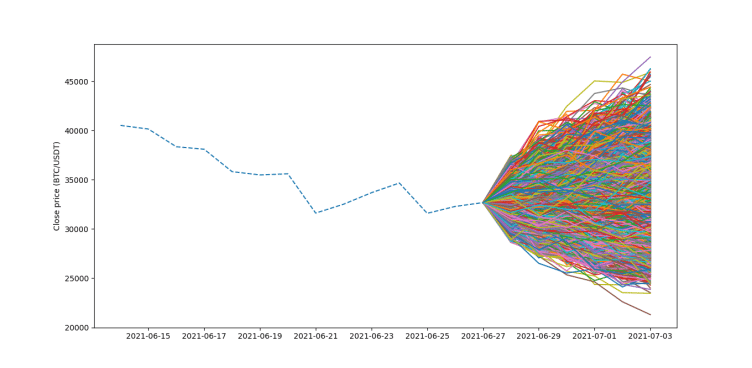
Figura 1: VaR por Montecarlo
Introducción
Las distribuciones de probabilidad, y en especial la distribución normal, constituyen una valiosa herramienta capaz de modelar fenómenos financieros como el rendimiento o la volatilidad de un activo para incrementar los beneficios reduciendo el riesgo.
Variable aleatoria y distribución de probabilidad
Primero, repasaremos los conceptos de variable aleatoria y distribución de probabilidad mediante un experimento que consiste en tirar dos dados 3000 veces. Como el resultado depende del azar se le denomina experimento aleatorio. Los sucesos elementales de nuestro experimento aleatorio son todas las posibles combinaciones en las que pueden reposar nuestros dos dados tras ser lanzados, y todos ellas forman el espacio muestral. En muchos experimentos aleatorios los resultados no son intrínsecamente numéricos; el número resulta de aplicar un instrumento de medida (función) al agente bajo estudio. A esa función se le denomina variable aleatoria.
Una variable aleatoria es una función que asigna un número a cada suceso elemental de un espacio muestral.
En nuestro caso el funcionamiento de la variable aleatoria es directo, asignará como número la suma de los puntos de las caras superiores de ambos dados tras cada lanzamiento. Por tanto nuestro espacio muestral es el siguiente:
E = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
Lo que nos lleva a repasar los dos tipos de variables aleatorias que podemos encontrar:
> Una variable aleatoria es discreta si sólo puede tomar una serie de valores concretos dentro de un rango, como los dos posibles resultados de tirar una moneda al aire.
> Una variable aleatoria es continua si puede tomar infinitos valores dentro de un intervalo numérico determinado, como la estatura de los jugadores de la NBA (1,68, 1.9234…).
Atendiendo a nuestro espacio muestral, concluimos que nuestra variable aleatoria es discreta. Sabiendo todo esto procedemos a realizar el experimento, tirando los dados y apuntando cada uno de los resultados. Al terminar los 3000 lanzamientos podemos indicar el número de veces que ha salido cada número en una tabla de frecuencias como en el Cuadro 1.
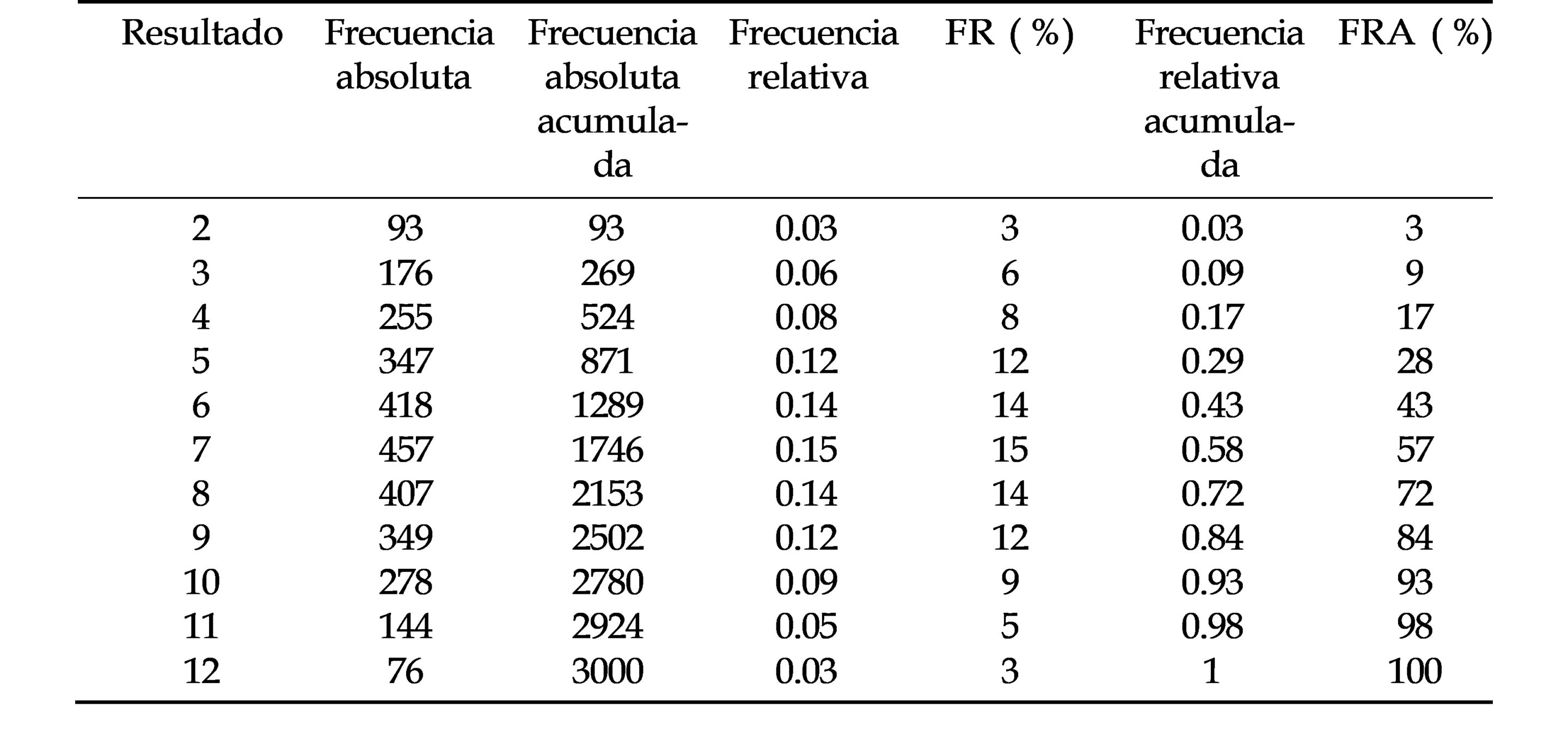
Cuadro 1: tabla de frecuencias
La información que nos proporciona el Cuadro 1 es la siguiente:
– Frecuencia absoluta: número de veces que se ha repetido un suceso elemental del espacio muestral.
– Frecuencia absoluta acumulada: suma acumulada de las frecuencias absolutas, es decir, el número total de observaciones que son menores o iguales a un valor específico del espacio muestral.
– Frecuencia relativa: proporción de veces que se repite un resultado
– Frecuencia relativa acumulada: suma acumulada de las frecuencias relativas, es decir, el porcentaje total de observaciones que son menores o iguales a un valor específico del espacio muestral.
Pero, ¿qué pasa si representamos la frecuencia absoluta o la relativa en un histograma? Lo podemos ver en las figs. 2 y 3.
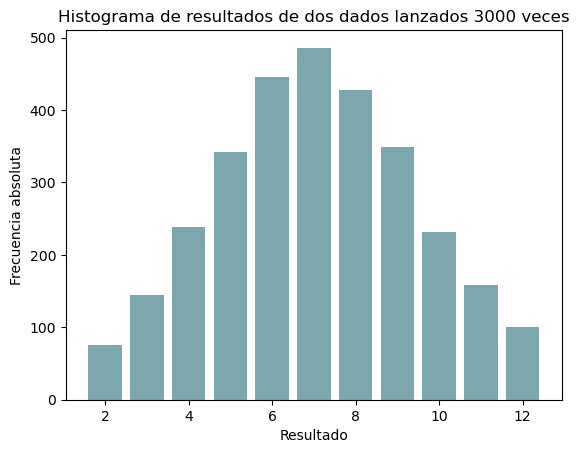
Figura 2: Distribución de frecuencias absolutas
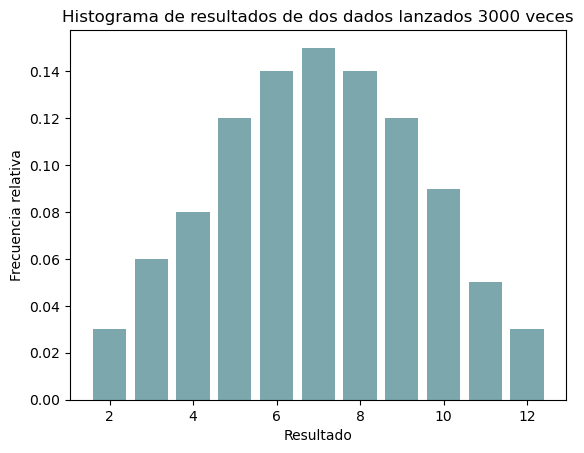
Figura 3: Distribución de frecuencias relativas
Esa forma recuerda a algo, ¿verdad? También podemos representar las frecuencias acumuladas (fig. 4); tal vez esta forma te suene menos que la anterior, ya veremos después.
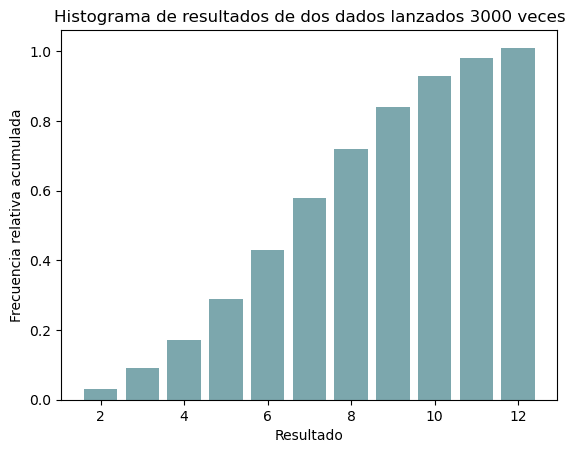
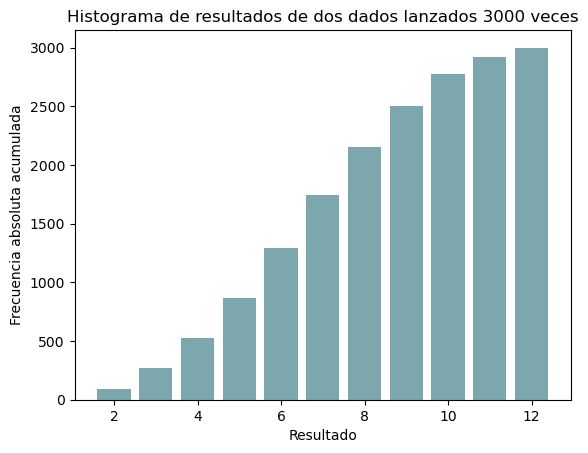
Figura 4: Frecuencias acumuladas
Pero sí, nuestra variable aleatoria sigue una distribución normal. Pero atención, nuestra variable aleatoria es discreta mientras que la distribución normal toma valores continuos, pero no importa porque la conclusión que quiero que saquemos de este experimento es que la distribución de una variable aleatoria continua no es mas que la conclusión lógica de tomar un número infinito de muestras y presentarlo en forma de histograma. Entonces, atendiendo de nuevo a la fig. 5, vemos que
Una distribución de probabilidad es una descripción matemática de la probabilidad de que una variable aleatoria tome un valor particular o caiga dentro de un intervalo de valores
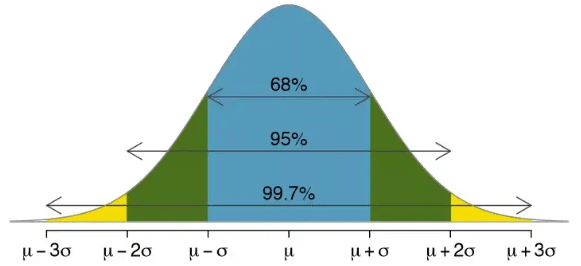
Figura 5: FDP Distribución normal
Para ello una distribución de probabilidad se compone de las siguientes funciones:
– La función de masa de probabilidad, se relaciona con la frecuencia absoluta de una variable discreta y describe la probabilidad de que una variable aleatoria discreta tome un valor determinado.
– La función de densidad de probabilidad (FDP), se relaciona con las frecuencias absolutas y relativas de una variable aleatoria discreta, y es la probabilidad de que una variable aleatoria continua tome un valor específico en un intervalo dado.
– La función de distribución acumulada (FDA), se relaciona con la frecuencia absoluta y relativa acumuladas de una variable aleatoria discreta, y es la probabilidad de que una variable aleatoria tome un valor menor o igual a un valor determinado.
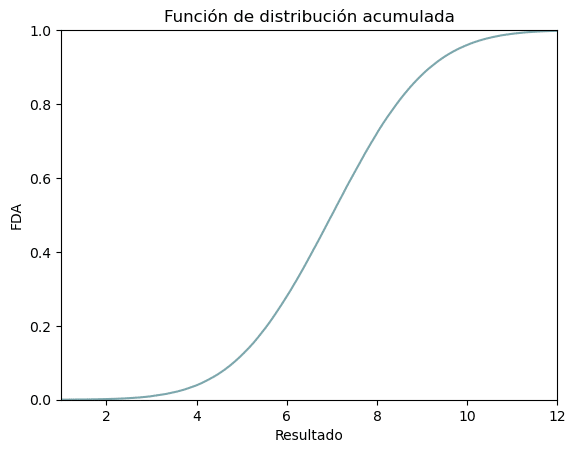
Figura 6: FDA distribución normal para μ= 0 y σ= 1,71
La distribución normal es una distribución de probabilidad continua cuya función de densidad de probabilidad tiene forma de campana de Gauss.
Vemos que la función de densidad de probabilidad de una distribución (fig. 5) está centrada en μ, siendo μ la media, y que sus intervalos mas significativos quedan determinados por la suma de μ con múltiplos de ±σ, que es la desviación estándar.
La desviación estándar es una medida de dispersión que mide la distancia promedio de cada valor de un conjunto de datos al valor promedio del conjunto.
El área que encierra el intervalo de la primera desviación estándar se encuentra el 68 % de los resultados obtenidos, hasta la segunda desviación estándar el 95 %, y hasta la tercera el 99.7 % Por otra parte, recordando los histogramas de las frecuencias relativas de nuestro experimento podemos deducir la forma que tendrá la función de distribución acumulada de la distribución normal de una variable aleatoria continua, y es la de la fig. 6. Si calculamos el área que va de 0 a un valor del eje “Resultado” por ejemplo 6.5, obtendríamos la probabilidad de que el experimento arrojará un valor menor o igual a 6.5.
Conclusión
En este articulo hemos adquirido una visión general de qué es una variable aleatoria, y de cómo nos valemos de la distribución de probabilidad para predecir sus resultados. Para ello hemos recurrido a la construcción de una tabla de frecuencias de un experimento aleatorio modelado por una variable aleatoria discreta que nos ha permitido dar el salto a la comprensión de la distribución de probabilidad de una variable aleatoria continua, todo ello enfocado en la distribución normal.
En finanzas, con la distribución normal (y otras distribuciones de probabilidad), podemos hacer suposiciones sobre los rendimientos futuros de un activo basándonos en rendimientos pasados. Si quieres saber cómo, en el próximo articulo nos adentraremos mas en la distribución normal, y aplicaremos un caso práctico de predicción de un activo financiero con una gráfica de tipo abanico (fan chart).
Referencias
González, J. J., Guerra, N., Quintana, M. P., & Santana, A. (sin año). Métodos estadísticos
Hall, B. (2020, 16 de agosto). The Normal Distribution, Confidence Intervals, and Their Deceptive Simplicity. Medium. Recuperado el 24 de febrero de 2023, de https://towardsdatascience.com/the-normal-distribution-confidence-intervals-and-their-deceptive-simplicity-eb4c6f9fadec
Fig.1- Leonardo Araujo
Fig.5 – Libre Text








