Introducción
Este es el segundo de una serie de artículos cuyo objetivo final es entender el Valor en riesgo por Montecarlo (VaR using Monte Carlo Simulation). El valor en riesgo es un estadístico muy potente que cuantifica el alcance de las posibles pérdidas de una empresa, cartera o posición durante un periodo de tiempo específico.
En el artículo anterior se adquirió una visión general de qué es una variable aleatoria, y de cómo nos valemos de la distribución de probabilidad para predecir sus resultados. También explicamos lo que significa que un experimento aleatorio siga una distribución normal.
En este artículo ampliaremos más nuestro conocimiento en estadística y en la distribución normal, conocimiento necesario para el análisis financiero. Después nos valdremos de esta distribución para predecir el comportamiento de un activo financiero por medio de la construcción de una gráfica de tipo abanico (fan chart) simplificada.
Estadísticos
El análisis financiero se basa en la capacidad de hacer estimaciones precisas sobre el comportamiento futuro de los activos financieros, haciendo estimaciones de parámetros de interés como el riesgo que llevan asociado o de su rendimiento esperado. Primeramente nos centraremos en los conceptos estadísticos aplicados a estos parámetros de interés.
La desviación estándar o desviación típica mide la dispersión de cada valor que toma el parámetro de interés de un activo con respecto a su conjunto de valores promedio. Se calcula como la raíz cuadrada de la varianza y se simboliza con 𝜎. Su fórmula para una distribución continua es la siguiente:
\sigma = \sqrt{\int_{-\infty}^{\infty} (x-\mu)^2 f(x) \, dx}
donde:
– x: variable aleatoria de la distribución, o los diferentes valores que va tomando el activo
– \mu: media de los valores del activo
– f(x): función de densidad de probabilidad del activo
Pero, ¿qué es la varianza?
La varianza es la media de las diferencias al cuadrado del conjunto de valores que toma el parámetro de interés de un activo con respecto a su media.
\sigma^2 = \int_{-\infty}^{\infty} (x-\mu)^2 f(x) \, dx
Profundizando más en la distribución normal
Las estimaciones financieras se basan en datos históricos y suposiciones sobre la distribución subyacente de los parámetros. Uno de los supuestos más comunes en las estimaciones es que los retornos se distribuyen de manera normal. Un activo que sigue una distribución normal de media 𝜇 y desviación estándar σ queda definido matemáticamente por la siguiente fórmula:
N(\mu,\sigma) \rightarrow f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}
Esta fórmula puede resultar intimidante, pero lo único que tenemos que tener en cuenta es que al pasarle el histórico del parámetro de interés de un activo ayudándonos de un ordenador nos devolverá una gráfica con forma de campana de Gauss, y que integrándola entre los instantes de tiempo que deseemos nos dará la probabilidad de que el parámetro tome un cierto valor con un cierto margen de error que se relaciona con los intervalos de confianza, los cuales veremos más adelante. Podemos ver la representación de la distribución normal en la figura 1 que presentábamos en el artículo anterior.
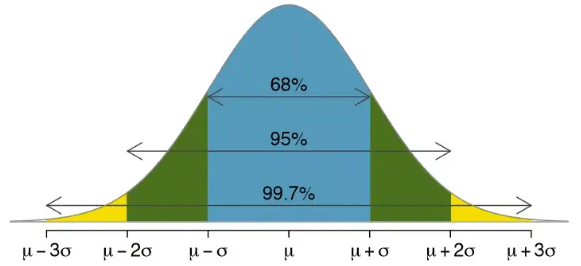
Figura 1: Distribución normal
> Curtosis
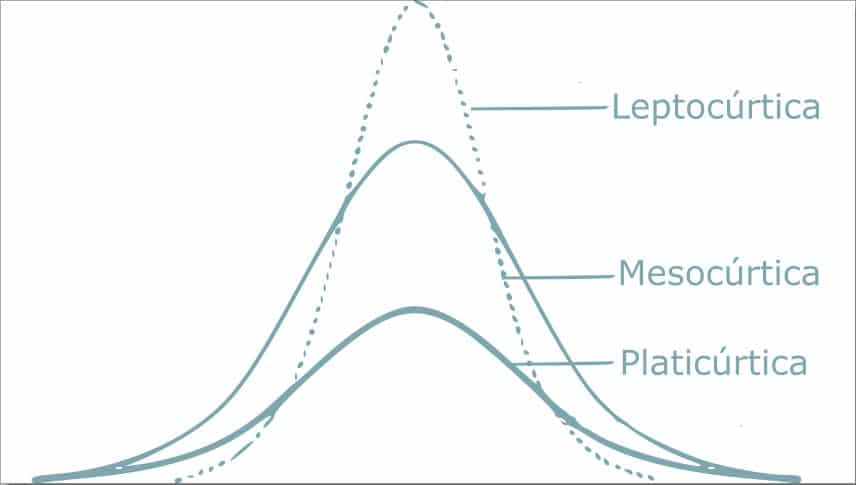
Cuanto mayor sea la concentración de muestras alrededor de la media, mayor será la desviación estándar, y viceversa. Esto afecta a la forma de la distribución normal dando lugar a tres tipos:
– Leptocúrtica: grado de concentración elevado, forma puntiaguda
– Mesocúrtica: grado de concentración medio
– Platicurica: bajo grado de concentración, forma achatada
> Sesgo
En algunos textos podremos encontrar un tipo de distribución que recuerda a la normal, pero con una cierta asimetría. Es la distribución sesgada (skewed distribution), y como su propio nombre indica, presenta un sesgo que puede ser positivo o negativo.
– Distribución normal: la media, moda y mediana son iguales, al igual que en otras distribuciones simétricas.
– Distribución sesgada a la derecha (sesgo negativo): media mayor que la mediana.
– Distribución sesgada a la izquierda (sesgo positivo): media menor que la mediana.
Decimos que el sesgo es positivo o negativo atendiendo hacia qué sentido del eje se estira la cola de la distribución.
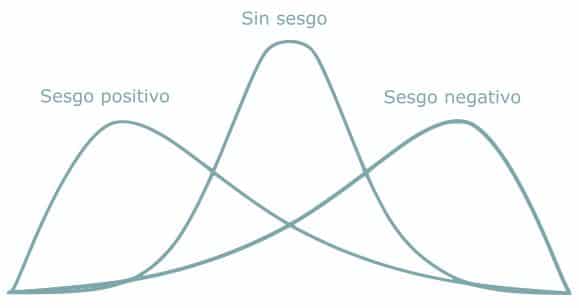
Figura 3: Funciones sesgadas
Predicción de un activo mediante la construcción de una Fan Chart aplicando la distribución normal
Si asumimos que el retorno de una acción cotizada se distribuye como una normal N (µ,σ²) podemos representar su movimiento futuro como un proceso de difusión que depende de la media (µ) y la volatilidad (σ).
Si la volatilidad permaneciera constante en el futuro e igual a su último valor registrado (dicha asunción se puede relajar usando modelos predictivos de volatilidad tipo GARCH), podemos usar el concepto de intervalo de confianza para dicho proceso de difusión. Utilizaremos un intervalo de confianza del 95%. Pero, ¿qué es esto del intervalo de confianza? Dada a la naturaleza cambiante y volátil de los mercados, es importante reconocer la presencia de incertidumbre en las estimaciones. Es aquí donde entran en juego los intervalos de confianza, que permiten medir y comunicar la incertidumbre asociada a una estimación. Un intervalo de confianza es un rango de valores plausible dentro del cual se espera que se encuentre el valor de interés del activo con cierto nivel de confianza. Aprender este concepto de forma rigurosa daría para un posible artículo, pero por el momento tendremos en cuenta que para la distribución normal los intervalos de confianza mas utilizados son 90%, 95% y 99%, debido a su balance entre precisión y exactitud.
Visto el concepto intervalo de confianza, continuamos con el cálculo. En t=0, calculamos una media y volatilidad de retornos históricos, lo que nos permite construir un intervalo de confianza para t=1 según la normal N(\mu_{t=0}, \sigma_{t=0}^2).
t=2 \rightarrow [N(\mu_{t = 2}, \sigma_{t = 2}^2)|t=0] = [N(\mu_{t = 0}, \sigma_{t = 0}^2)] + [N(\mu_{t = 1}, \sigma_{t = 1}^2)|t=0]\\ = [N(\mu_{t = 0}+\mu_{t = 1}, \sigma_{t = 0}^2+\sigma_{t = 0}^2)|t=0]
Esto nos daría el intervalo de confianza de un proceso que va desde t=0 a t=1. Para calcular el intervalo de confianza en t=2, necesitamos calcular la distribución normal en t=1, con su media \mu_{t=1} que incorpora la media de predicciones en t=1 del paso anterior y la misma \sigma=\sigma_{t=0} constante. La normal N(\mu_{t=1}, \sigma_{t=1}^2) nos daría el intervalo de confianza de un proceso que va de t=1 a t=2. Para calcular el intervalo de confianza de un proceso que va desde t=0 a t=2 tenemos que tener en cuenta las dos distribuciones condicionales, la de t=0 a t=1 y la de t=1 a t=2, que al asumir que el retorno de la acción sigue una distribución normal, nos permite calcular la distribución compuesta como la suma de las dos distribuciones condicionadas (solo es posible al ser normal).
t=2 \rightarrow [N(\mu_{t = 2}, \sigma_{t = 2}^2)|t=0] = [N(\mu_{t = 0}, \sigma_{t = 0}^2)] + [N(\mu_{t = 1}, \sigma_{t = 1}^2)|t=0]\\ = [N(\mu_{t = 0}+\mu_{t = 1}, \sigma_{t = 0}^2+\sigma_{t = 0}^2)|t=0]
con \mu_{t = 2}=\mu_{t = 0}+\mu_{t = 1} y \sigma_{t = 2}^2=\sigma_{t = 0}^2+\sigma_{t = 0}^2=2\sigma_{t = 0}^2 y donde vemos que las medias y varianzas se suman directamente. La varianza se puede sumar al suponer que es constante e igual a la última medición \sigma_{t = 0} para futuros instantes de tiempo. En el caso de los intervalos de confianza, usamos la desviación estándar. Esto lleva a \sigma_{t=2}^2=2\sigma_{t=0}^2 y \sigma_{t=2}=\sqrt{2\sigma_{t=0}^2}=\sqrt 2\sigma_{t=0}. La desviación estándar acaba siendo igual a la raíz del número de saltos temporales previos (el número de normales condicionales previas) multiplicada por la última medición de desviación estándar.
t = 2 \rightarrow IC_{95\%} = [\mu_{t=2} - 2\sigma_{t=2}, \mu_{t=2}+2\sigma_{t=2}]\\ =[\mu_{t=2} - 2\sqrt 2\sigma_{t=0}, \mu_{t=2}+2\sqrt 2\sigma_{t=0}]\rightarrow N(\mu_{t=2},\sigma_{t=2}^2)
Generalizando este proceso para cualquier horizonte temporal t:
t \rightarrow [N(\mu_{t = t}, \sigma_{t = t}^2)|t=0]=\\ = [N(\mu_{t = 0}, \sigma_{t = 0}^2)] + [N(\mu_{t = 1}, \sigma_{t = 1}^2)|t=0]+\dots +[N(\mu_{t = (t-1)}, \sigma_{t = t}^2)|t=0]\\ = [N(\mu_{t = 0}+\mu_{t = 1}+\dots+\mu_{t = (t-1)}, \sigma_{t = 0}^2+\sigma_{t = 0}^2+\dots+\sigma_{t = 0}^2)|t=0]\\ \mu_{t = t}=\mu_{t = 0}+\mu_{t = 1}+\dots+\mu_{t = (t-1)}\\ \sigma_{t = t}^2=\sigma_{t = 0}^2+\sigma_{t = 0}^2+\dots+\sigma_{t = 0}^2=(t)\sigma_{t = t}^2
Se suma t veces la última varianza medible de forma constante. Siguiendo el proceso anterior:
t \rightarrow IC_{95\%} = [\mu_{t=t} - 2\sigma_{t=t}, \mu_{t=t}+2\sigma_{t=t}]\\ =[\mu_{t=t} - 2\sqrt{t}\sigma_{t=0}, \mu_{t=t}+2\sqrt{t}\sigma_{t=0}]\rightarrow N(\mu_{t=t},\sigma_{t=t}^2)
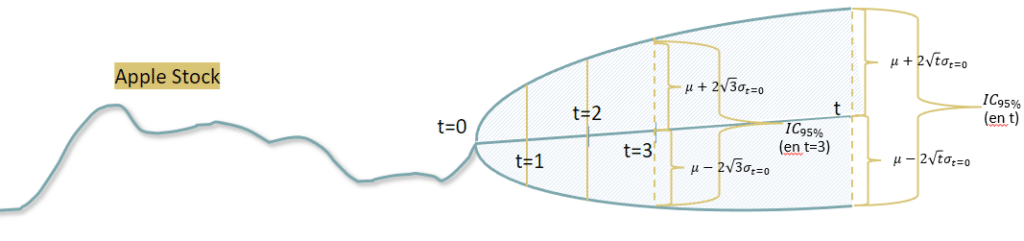
Aplicando este proceso para un activo real seríamos capaces de construir una gráfica de tipo abanico simplificada (fan chart) como la de la gráfica 1, que nos muestre de forma clara nuestro parámetro de interés de un activo para ayudarnos en la toma de decisiones financieras. Es simplificada porque solo tiene en cuenta un intervalo de confianza.
Conclusión
En este artículo hemos profundizado mas en la distribución normal y hemos utilizado ese conocimiento para estimar el comportamiento de un activo financiero. Después hemos representado el resultado del procedimiento en una gráfica de tipo abanico simplificada (fan chart), un artefacto muy utilizado en finanzas para visualizar y comunicar la incertidumbre asociada a las proyecciones futuras de un activo. Asentar estos conocimientos de análisis financiero básico sin duda nos aporta un punto de partida para entender esta potentísima disciplina. En el próximo artículo trataremos el VaR por Montecarlo.
Referencias
Wackerly, D., Mendenhall, W., y Scheaffer, R. (2021). Estadística Matemática (7th ed.).
Fanny Zapata. (15 de diciembre de 2022). Curtosis: definición, tipos, fórmulas, para qué sirve, ejemplo. Recuperado de https://www.lifeder.com/curtosis/
Fig.1- Araujo, L. (2020, August 24). Bitcoin price forecasting with Monte Carlo simulations. Recuperado de https://www.linkedin.com/pulse/bitcoin-price-forecasting-monte-carlo-simulations-leonardo-araujo/?trk=articles_directory
Fig.2- Keim, R. (2020, August 24). Understanding Parametric Tests, Skewness, and Kurtosis. All About Circuits. Recuperado de https://www.allaboutcircuits.com/technical-articles/understanding-the-normal-distribution-parametric-tests-skewness-and-kurtosis/
Fig.3- Keim, R. (2020, August 24). Understanding Parametric Tests, Skewness, and Kurtosis. All About Circuits. Recuperado de https://www.allaboutcircuits.com/technical-articles/understanding-the-normal-distribution-parametric-tests-skewness-and-kurtosis/








