PUBLICACIÓN EN JOURNAL: Metodología de Optimización de Carteras incluyendo información de sus dinámicas mediante sensibilidades aproximadas con redes neuronales
Introducción
Esta es la introducción a una serie de entradas al blog que explicarán en detalle el Paper publicado recientemente por el equipo de Análisis e Investigación Cuantitativa de Miraltabank en el Journal of Machine Learning with Applications, al cual se puede acceder en el link junto con códigos de programación y conjuntos de datos para que el usuario pueda realizar experimentos o mejorar su gestión del riesgo en inversiones.
Comentario
En este artículo se presenta un marco teórico en el cual, las dinámicas causales de los activos se pueden modelizar por medio de ecuaciones en derivadas parciales (los principales modalizadores del universo) y su solución, así como las derivadas parciales aproximarse mediante redes neuronales. Por medio del principio de causalidad común de Hans Reichenbach (1956), el único caso en el que correlación se puede usar para aproximar causalidad, obtenemos los drivers o fuentes de causalidad óptimos para una cartera, siendo estos aquellos que están correlacionados en mayor medida con el mayor número de constituyentes de la cartera.
Dada una cartera de activos cualquiera y de una base de datos con miles de candidatos de una muestra del mercado global con todo tipo de indicadores y productos cotizados seleccionamos los drivers causales óptimos para dicha cartera. Esto nos permite aproximar las derivadas parciales, sensibilidades, de cada uno de los activos de la cartera respecto de los mismos drivers comunes causales de la cartera. Una vez obtenidas dichas sensibilidades, podemos definir un espacio geométrico de sensibilidades sobre el que proyectar los retornos de los activos de la cartera. Esto nos permite definir una matriz de distancia, al igual que la correlación es una matriz de distancia, y la llamamos matriz de sensibilidades. Dicha matriz nos permite resolver el problema de optimización de carteras incluyendo información de las sensibilidades de los activos respecto a las fuentes causales de sus dinámicas y las de la cartera.
Metodología del modelo
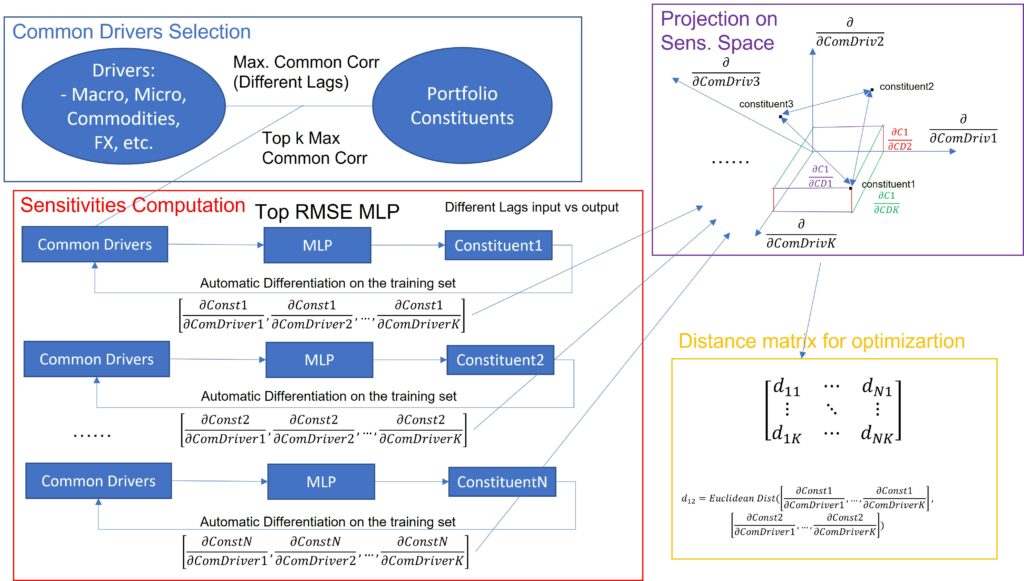
- Fuente: Rodríguez Domínguez, Alejandro (2023): “Portfolio optimization based on neural networks sensitivities from asset dynamics respect common drivers.” Machine Learning with Applications, Vol. 11, No. 15. Available at https://doi.org/10.1016/j.mlwa.2022.100447.
- Descripción: Selección de Drivers de la cartera óptimos (Azul); cálculo de sensibilidades con diferenciación automática en Redes Neuronales (MLP) respecto a dichos drivers(Rojo);proyección de los constituyentes de la cartera en el espacio de sensibilidades (Morado); computo de la matriz de distancias en dicho espacio (Matriz de sensibilidades) para optimizar diversificación (Amarillo).
Esto hace que el problema de diversificación presentado inicialmente por Markowitz (1952) presente una nueva dimensionalidad de direccionalidad temporal o trayectoria no contemplada anteriormente. Con ello conseguimos unos retornos ajustados por riesgo mejores que todos los métodos competidores. También conseguimos una metodología capaz de sustituir la inversión por factores estadísticos, los cuales pueden ser espurios o estacionarios, por variables que son fuentes causales de las dinámicas de la cartera y que son públicas y cotizadas a diario, y cambiantes, reduciendo así el coste de computación y monetario que supone la inversión por factores.
Por último, este marco teórico-practico de gestión de carteras abre las puertas a nuevas investigaciones en las que mejorar la aproximación de las dinámicas de los activos y de sus sensibilidades. Para ello se pueden usar ecuaciones diferenciales estocásticas, muy usadas en finanzas desde hace medio siglo, así como nuevas definiciones de las sensibilidades que permitan mejores aproximaciones de las dinámicas causales y trayectorias del riesgo de los activos.
En el siguiente enlace encontrarán el paper publicado, y en la sección “Data Avaliability” un ambiente ya en funcionamiento con el que conocedores de lenguaje Python podrán hacer experimentos con muchos modelos de optimización de carteras incluido el nuestro, en más de 10 años de datos diarios y con acceso a cientos de drivers de mercado.
Referencias
Markowitz, Harry. “Portfolio Selection.” The Journal of Finance, vol. 7, no. 1, 1952, pp. 77–91. JSTOR, https://doi.org/10.2307/2975974. Accessed 18 Jan. 2023.
Reichenbach, H. (1956). The direction of time (Vol. 65). Univ of California Press.
Rodríguez Domínguez, Alejandro (2023): “Portfolio optimization based on neural networks sensitivities from asset dynamics respect common drivers.” Machine Learning with Applications, Vol. 11, No. 15. Available at https://doi.org/10.1016/j.mlwa.2022.100447.
Glosario
principio de causalidad común de Hans Reichenbach
Teoría de Portafolio Moderna (Modern Portfolio Theory)








