A lo largo de los últimos artículos se ha destacado el uso de algoritmos o técnicas cuantitativas (Inteligencia Artificial, VaR, fan chart…) dentro del sector bancario y financiero. Estas técnicas se basan en herramientas matemáticas ampliamente utilizadas y de gran calado dentro de la industria. La revolución técnica que ha tenido lugar en el mundo financiero ha dado lugar a que perfiles como ingenieros, matemáticos, físicos o estadísticos hayan ido ganando un papel decisivo a la hora de definir estrategias cuantitativas y que, como consecuencia, las herramientas a emplear se hayan diversificado enormemente con excelentes resultados (Zuckerman, 2019).

Sin embargo, en recientes artículos no se han mencionado el conocido como movimiento browniano. Esta herramienta supuso una auténtica revolución dentro del mundo financiero al permitir el desarrollo de modelos con una capacidad de replicar o simular la incertidumbre de los movimientos en los mercados de una manera sistemática.

Movimiento browniano

Un movimiento browniano consiste, brevemente, en un camino aleatorio a lo largo del tiempo. Por ejemplo, las partículas que componen los gases siguen movimientos brownianos, pues su trayectoria no sigue un rumbo predecible en tanto que se comportan de manera aleatoria chocando unas con otras.

Para comprender de manera sencilla lo que es un movimiento browniano, puede simularse fácilmente una aproximación superficial con una herramienta como Excel al definir una función que varía en -1 o +1 respecto a su anterior valor en función de si un número aleatorio generado mediante el comando “ALEATORIO()” es menor o mayor que 0.5, respectivamente.

=SI(ALEATORIO()<0,5;B3+1;B3-1)

Así, se puede obtener una gráfica como la que sigue cuando se parte de un valor inicial de 0 en, por ejemplo, la celda B3 de una hoja Excel y se arrastran valores:

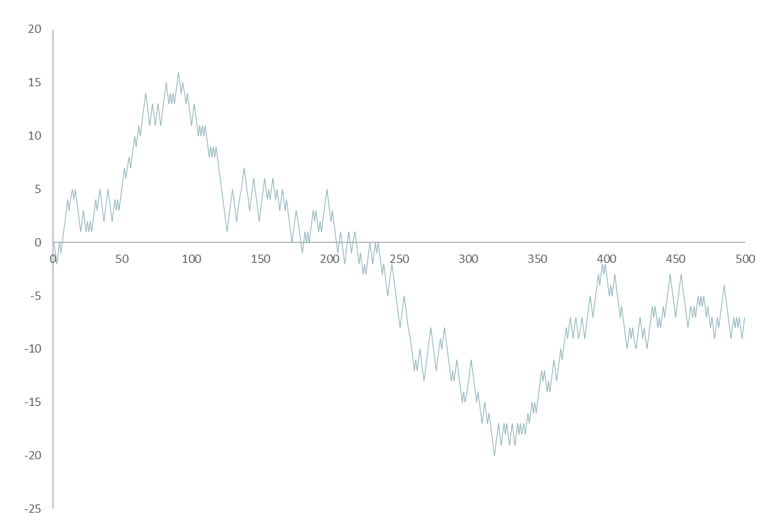
Tal y como se puede ver, el camino seguido es errático (y no predecible), pues no sigue una tendencia clara o una evolución que se pueda definir sin prescindir del término aleatorio del que parte. Este término, desconocido a priori y variable en cada nuevo camino generado, es lo que distingue un proceso como este de uno cuya trayectoria podamos conocer de antemano, es decir, de un proceso determinista.

Si bien la relación de este tipo de procesos con la historia de la probabilidad es estrecha y se remonta a hace siglos, uno de los procesos basados en el movimiento browniano que más nos interesan para este artículo es el proceso Wiener, el cual es, dicho de alguna manera, una expresión matemática del movimiento browniano.

Este proceso sigue una serie de propiedades algo más complejas que el ejemplo de Excel, pero que, en esencia, sigue una filosofía similar: variaciones aleatorias en diferentes y sucesivos instantes de tiempo infinitamente pequeños -infinitesimales-.

Proceso Wiener

El movimiento browniano encuentra su expresión matemática en el famoso proceso Wiener (dW_t), que parte de una serie de cuatro propiedades características (Mikosch 1999):

• Empieza en W_0 = 0
• Tiene incrementos estacionarios e independientes.
• Para todo t > 0, W_t tiene una distribución N(0, t)
• Tiene caminos continuos, sin saltos.

¿Qué quiere decir todo esto? Que un proceso Wiener es una función que empieza con un valor 0 y cada paso temporal (cada instante definido en su evolución) sufre variaciones que son estacionarias e independientes entre ellas. Además, cada variación en el momento  sigue una distribución normal con media 0 y desviación típica t, es decir, que cuanto más aumenta el tiempo, más se desvían el conjunto de caminos que generemos del valor 0 inicial, pese a que la media de todos siempre tienda a ser 0.

Cabe mencionar que existe, desde que se desarrollaron estos modelos, debate acerca de si el uso de la distribución normal para definir los saltos es o no adecuada. Téngase en cuenta, por ejemplo, que esta distribución minimiza la posibilidad de ocurrencia eventos extremos o Cisnes Negros: eventos extremadamente adversos y altamente difíciles de predecir que ocurren con baja probabilidad, pero con consecuencias devastadoras; la crisis de 2008 es un buen ejemplo (Taleb 2011).

Si graficamos una representación del camino que sigue un hipotético proceso Wiener podríamos obtener la siguiente representación:

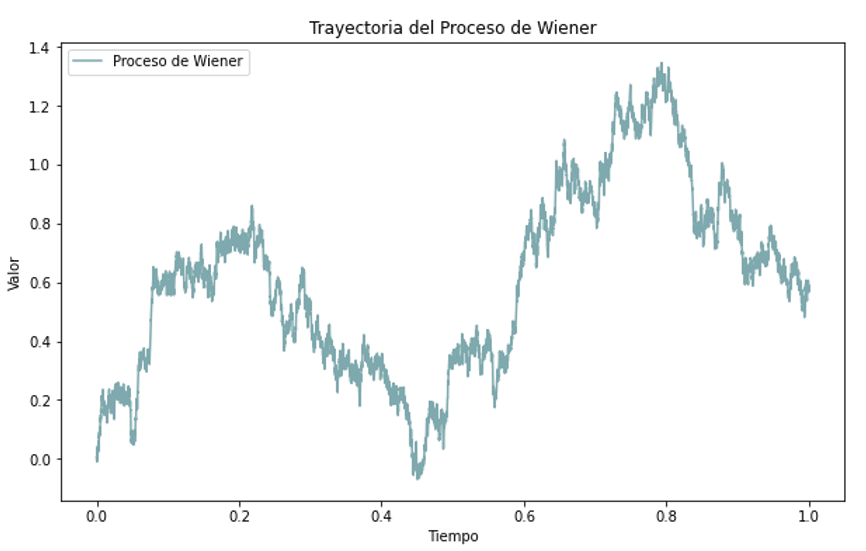
Un vistazo rápido da una primera impresión acerca de la utilidad de este tipo de procesos; su recorrido es similar al que podríamos ver en, por ejemplo, índices bursátiles, incluso cuando realmente no se ha seguido ningún criterio de simulación más allá de representar puramente un camino que seguiría el proceso para una realización.

Volviendo a su similitud con las evoluciones temporales dentro de los mercados bursátiles, véase, por ejemplo, una gráfica de la evolución del Ibex 35 reciente:

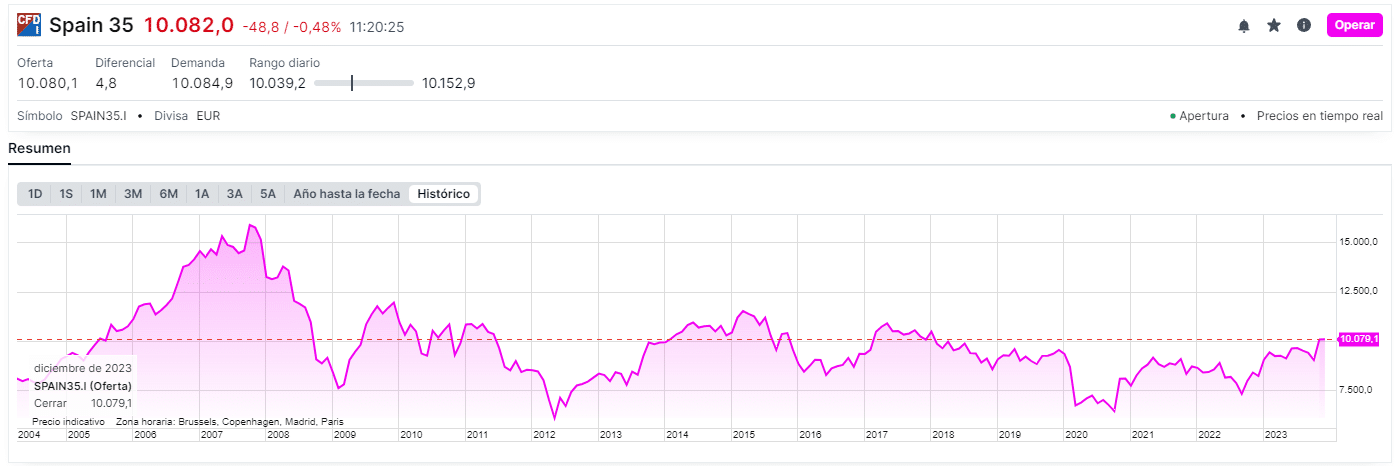
Por pura intuición, el lector puede comprender que, desarrollando modelos que partan de este tipo de bases teóricas, es posible obtener herramientas muy útiles para simular el comportamiento de los mercados.

El movimiento browniano es protagonista en los modelos financieros de la generación del proceso difusivo. Esto es, básicamente, la generación de variables aleatorias a lo largo del tiempo, ocurriendo a pequeña escala (infinitesimal), lo que dota al proceso de cambios continuos impredecibles.

Aplicaciones del proceso Wiener

La importancia del proceso Wiener es notable desde hace años y en él se han basado modelos de valoración de opciones (Black-Scholes), de evolución de tipos de interés (Vasicek) o de volatilidad estocástica (Heston). Este último, de mayor complejidad conceptual al asumir la volatilidad como variable en el tiempo.

En el caso de Black-Scholes, por ejemplo, el precio del subyacente ( ) viene dado por la ecuación diferencial estocástica:

dS_t=\mu S_t dt + \sigma S_t dW_t

Que se denomina proceso browniano geométrico. Sin entrar en demasiados detalles, podemos identificar que la parte de “ruido” introducida por el proceso de Wiener ( ) es:

\sigma S_t dW_t

Que básicamente representa la parte aleatoria introducida en el camino que se genere. A mayor valor de la volatilidad, σ, mayor “ruido” se introduce. La otra parte de este proceso:

\mu S_t dt

Representa la deriva, drift o parte determinista, la cual es constante y varía de manera predecible con el tiempo cuando la volatilidad es nula.

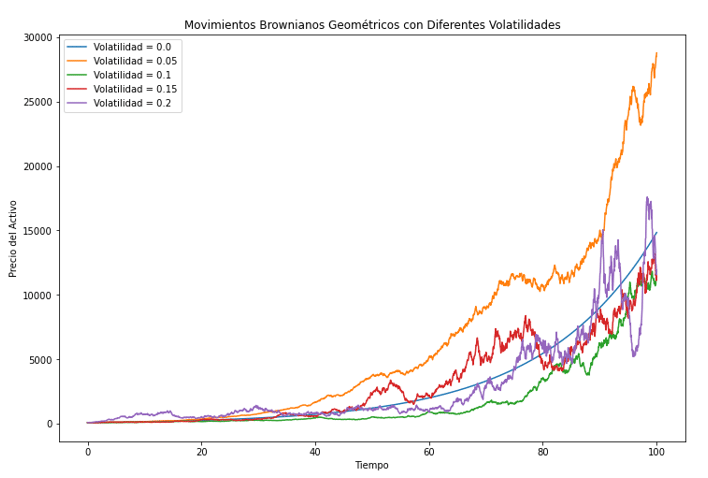
En la figura anterior puede observarse cómo cuando la volatilidad es cero, la trayectoria es completamente exponencial, sin variaciones aleatorias. Esto es lo esperable, pues al anular la adición de ruido dado por el proceso Wiener, la función sigue la trayectoria geométrica que da nombre a este proceso particular. La comprensión de este fenómeno será muy útil para el apartado en donde se trate el proceso de Lévy.

La aportación del movimiento browniano a estos modelos es, como se ha dicho, el proceso difusivo, es decir, el añadir ruido o aleatoriedad a las trayectorias, y consiguiendo así que la modelización sea más fiel a la realidad del mundo financiero, donde las variaciones tienen un alto componente impredecible.

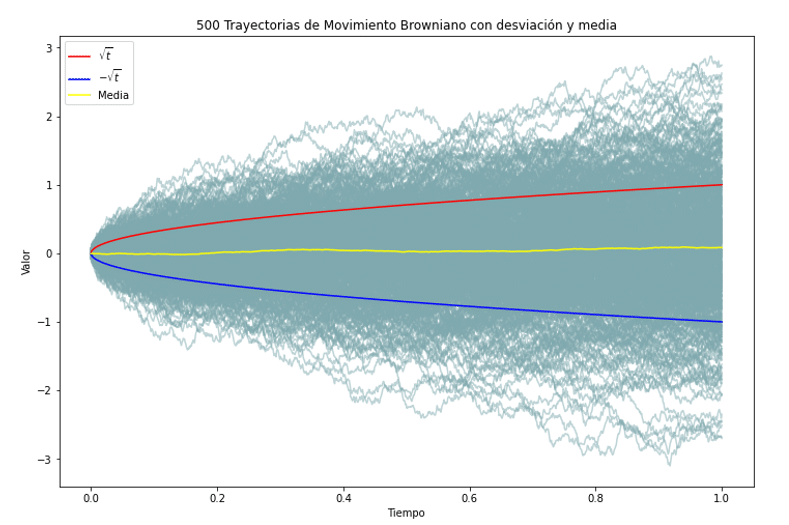
En la anterior gráfica, puede observarse el fenómeno de la aleatoriedad inherente a este proceso al graficar 500 trayectorias diferentes para un proceso puro de movimiento browniano. Tal y como se puede ver, el proceso difusivo se genera en tanto que los caminos seguidos son meramente probabilísticos, sin que haya un proceso determinista que se repita. Los análisis de media y desviaciones muestran cómo sí que existen tendencias -en sintonía con lo explicado previamente- que se dan dentro del proceso, pero que no dejan de tener un gran componente de aleatoriedad.

Propiedades características del proceso Wiener

Una característica especial del movimiento browniano y que suele ir contra lo acostumbrado a ver ya en asignaturas de matemáticas a nivel de bachillerato es que, pese a ser una trayectoria continua, no es diferenciable. En otras palabras, partiendo de la metodología usual de cálculo de pendientes en un punto -y, como consecuencia, de su recta tangente- no se puede llegar a dicho resultado en una trayectoria browniana, pese a que sea continua.

Un clásico ejemplo de esto suele presentarse con la función y = |x| que define el valor absoluto de la variable independiente x. Esta función presenta en el valor x = 0 un fenómeno conocido como codo, que impide calcular una derivada en ese punto, pues admitiría infinitas trayectorias.

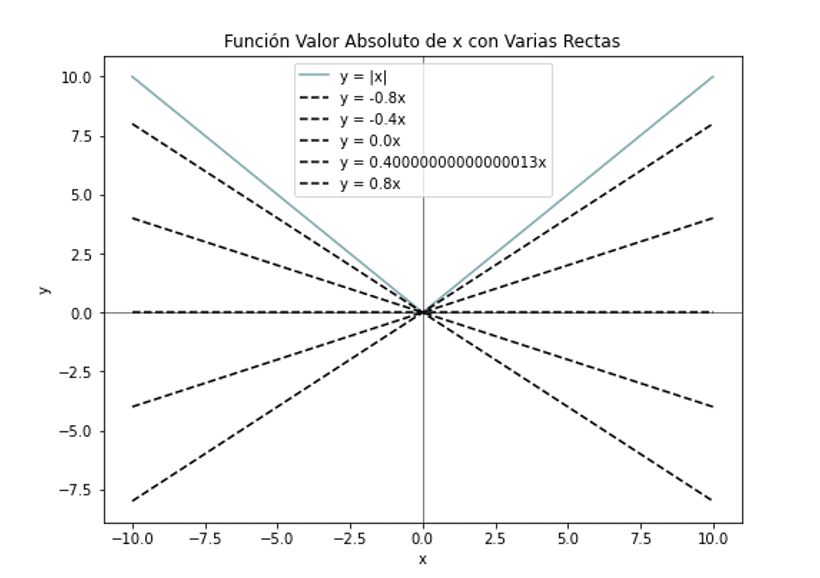
Tal y como se puede ver en la figura anterior, las posibilidades son infinitas. Si bien este no es exactamente el caso del movimiento browniano, sí es intuitivo para introducir cómo una función, pese a ser continua, pueda no ser diferenciable en según qué puntos.

El caso del movimiento browniano es más complejo, pues aquí se pone en juego la parte no determinista de su naturaleza, cosa que no ocurre en la función valor absoluto, que sí es determinista al no tener un componente aleatorio -para un valor de , siempre vamos a saber el valor de y.

En este punto cabe recordar que el movimiento browniano se crea a través de variaciones infinitesimales -es decir, que tienden a tener un valor cero- a lo largo del tiempo. Estas variaciones no están definidas por ninguna función determinista, pues son aleatorias (recordemos que siguen una distribución normal), por lo que, ¿cómo vamos a calcular la recta tangente a punto si ese punto es aleatorio? No podemos saber algo sobre una trayectoria que no conocemos a priori, como sí es el caso de funciones deterministas, continuas y diferenciables. Si bien excede el propósito de este artículo, la demostración matemática existe y es fácilmente visualizable en internet (McKnight 2009).

Otra propiedad interesante del movimiento browniano es la conocida como escalamiento fractal. Básicamente, esta característica significa que da igual las escalas temporales que tomemos para observar la trayectoria del movimiento browniano, pues las trayectorias que observemos siempre van a ser similares entre ellas y estadísticamente.

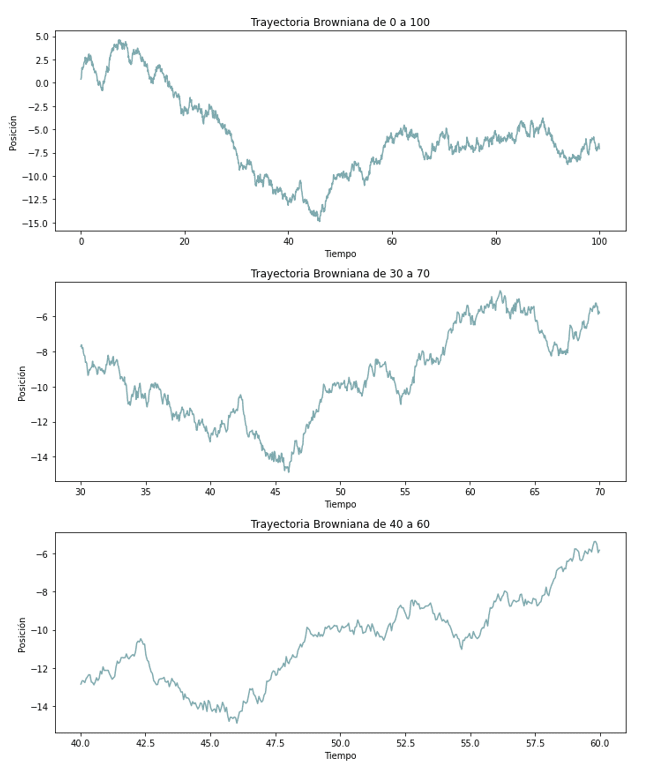
Tal y como se puede observar en la figura anterior, para una misma trayectoria se observan llamativas similitudes al variar los intervalos temporales en donde se representa. Este fenómeno se relaciona con la teoría de fractales y muestra una naturaleza interna menos aleatoria al tener estructuras más coherentes.

Proceso de Lévy

Hasta ahora nos hemos centrado en el movimiento browniano y su expresión matemática, el proceso Wiener. Hemos descrito casos de uso de este último en modelos financieros a través de procesos como el browniano geométrico, destacando la parte determinista, de la mano del drift o tendencia, y la parte aleatoria, generada por el ya mencionado proceso de Wiener.

Sin embargo, dentro de la modelización en el mundo financiero, existe el conocido como proceso de Lévy, que aúna diferentes aspectos muy interesantes a la hora de predecir el comportamiento de los mercados financieros.

Por un lado, el proceso de Lévy se compone -como no podría ser de otra manera- de un proceso difusivo dado por un proceso de Wiener. Por otra, tiene, al igual que el movimiento browniano geométrico, una aportación de tendencia o drift.

El aspecto novedoso de este proceso es la inclusión de saltos en los valores aleatorios tanto en magnitud como en frecuencia, ¿qué queremos decir con saltos y en qué se diferencia de un proceso Wiener? La respuesta es sencilla: mientras que en el proceso Wiener tenemos variaciones continuas en tiempo con su respectiva distribución de probabilidad, en el proceso de Lévy la inclusión de saltos implica la existencia de discontinuidades al sufrir variaciones bruscas en momentos aleatorios.

Si bien la notación matemática se vuelve más compleja en este modelo (Papapantoleon 2008) podemos realizar una explicación visual para ayudar a comprender este fenómeno.

Vamos a descomponer un proceso de Lévy en sus tres partes constituyentes. El ejercicio consistirá en definir una parte asociada únicamente a un movimiento browniano o proceso Wiener -parte difusiva-, una parte asociada a los saltos mencionados y, por último, una parte de tendencia o drift -parte constante en este caso:

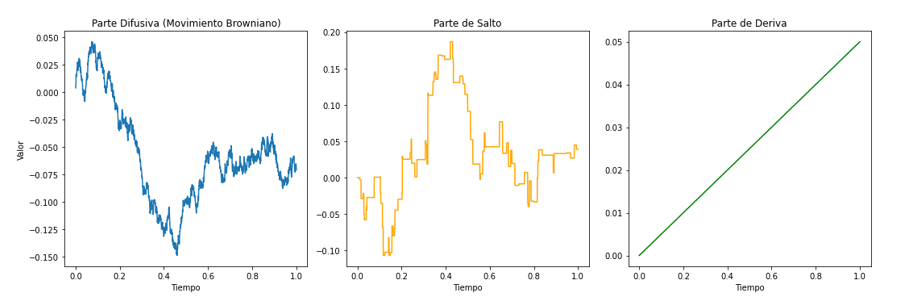
Una vez tenemos estos valores, constituyentes por separado de las partes que componen el proceso de Lévy, podemos sumar para obtener el camino seguido:

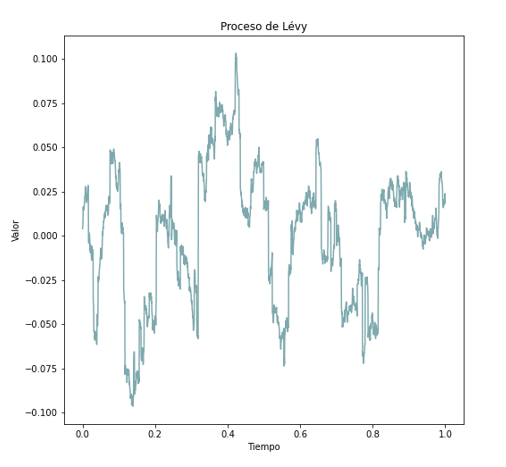
Tal y como se puede apreciar, esta representación de la evolución de un valor se diferencia notablemente de procesos vistos anteriormente, pues la inclusión de saltos aleatorios en el tiempo y de valor aleatorio también supone el añadir movimientos mucho más abruptos e impredecibles.

Similitudes y diferencias entre el proceso Wiener y el proceso de Lévy

Las similitudes y diferencias entre los dos procesos mencionados son claras en el momento en el que uno se construye a partir del otro.

El proceso Wiener constituye únicamente un proceso difusivo que genera caminos aleatorios de manera continua y con incrementos infinitesimales asociados a una distribución normal.

El proceso Lévy se compone de este proceso y, a mayores, incorpora un valor de tendencia constante en el tiempo, con la adición de un proceso generador de saltos en momentos aleatorios y de magnitud también variable.

Lógicamente, el proceso de Lévy es más útil a la hora de modelizar fenómenos financieros, pues su composición en proceso difusivo, tendencia y saltos aleatorios puede adecuarse más a las dinámicas de estos. El proceso Wiener no deja de ser la base de este y otros muchos modelos, pero con la carencia de representar únicamente la parte difusiva, es decir, de ruido.

Ambos procesos, pero especialmente el de Lévy, posee propiedades matemáticas mucho más complejas que las aquí expuestas, pero por exceder el propósito de este artículo el describirlas se dejan referencias a disposición del lector (Raible, 2000).

Aplicaciones

El proceso de Lévy se diferencia especialmente respecto a otros procesos como el movimiento browniano o el browniano geométrico por conseguir captar variaciones abruptas en su trayectoria de la mano de los saltos aleatorios y discontinuos, lo que unido a sus otras partes constituyentes lo hace especialmente útil para modelizar la evolución de valores que sufren cambios poco predecibles, pero de hondo calado en su trayectoria.

En los mercados financieros, esto puede imaginarse fácilmente de la mano de activos cuyos precios se ven sensiblemente alterados en momentos puntuales por noticias relevantes o acontecimientos geopolíticos. ¿Se imagina el lector algún ejemplo? Existe uno que sale constantemente en los telediarios y del que depende en gran parte la economía: el petróleo.

Los precios del petróleo siguen procesos que podríamos asumir como parecidos a los que describiría un proceso de Lévy ya que, sumado a pequeñas fluctuaciones diarias, su valor se ve afectado en gran parte por los acontecimientos del día a día: guerras, pandemias…

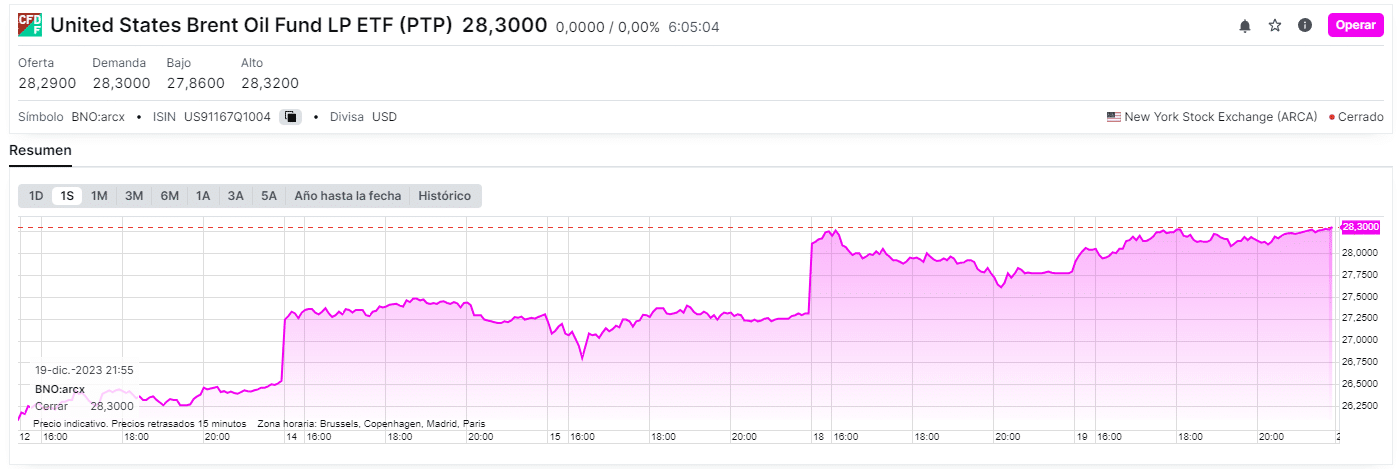
Tal y como se puede ver en la anterior gráfica, la evolución que ha seguido el precio del petróleo a lo largo del tiempo presenta una notable presencia de saltos abruptos que lo hacen susceptible de ser modelizado con un proceso de Lévy. Existen ejemplos de uso de este tipo de procesos en relación con su aplicación a los mercados financieros; por ejemplo, empleando este tipo de procesos para modelizar el comportamiento del precio del petróleo y valorar opciones con este como subyacente (Shahmoradi et al. 2016).

Conclusión

Se han presentado el proceso Wiener y el proceso Lévy, indicando sus propiedades y aplicaciones en el ámbito financiero. Si bien el proceso Wiener es la base de la modelización de procesos difusivos, otros procesos más complejos como el de Lévy son capaces de modelizar fenómenos de mayor complejidad al incorporar evoluciones más allá de la puramente difusiva.

Referencias

Zuckerman, G. (2019). The Man Who Solved the Market. Penguin Publishing Group.

Mikosch, T. (1999). Elementary Stochastic Calculus with Finance in View (vol.6). Advanced Series on Statistical Science and Applied Probability. World Scientific.

Taleb, N. (2011). El Cisne Negro. Paidós Ibérica.

McKnight, A. (2009). Some Basic Properties of Brownian Motion.

Papapantoleon, A. (2008). An Introduction to Lévy Processes with Applications in Finance. arXiv:0804.0482.

Raible, S. (2000). Lévy Processes in Finance: Theory, Numerics, and Empirical Facts. Semantic Scholar, Corpus ID: 150423027.

Shahmoradi, A. et al. (2016).  Pricing Crude Oil Options Using Lévy Processes. Journal of Energy Markets (vol. 9, No. 1). SSRN.