Este es el tercero de una serie de artículos cuyo objetivo final es entender el Valor en riesgo por Montecarlo (VaR using Monte Carlo Simulation). El valor en riesgo es un estadístico muy potente que cuantifica el alcance de las posibles pérdidas de una empresa, cartera o posición durante un periodo de tiempo específico.
En el artículo anterior se profundizó en aspectos de la distribución normal como la curtosis y el sesgo y se utilizó el concepto de gráfica de tipo abanico “fan chart” para visualizar la incertidumbre asociada a las proyecciones futuras de un activo. (Puedes verlo aquí)
En este artículo ampliaremos más nuestro conocimiento en predicción financiera para entender la Simulación de Montecarlo y con ella predecir la trayectoria futura de la curva correspondiente a los precios final de día de un activo financiero.
Origen
La simulación de Montecarlo fue desarrollada por John von Neumann y Stanislaw Ulam en el Laboratorio Nacional de Los Álamos mientras trabajaban en el proyecto Manhattan, centrado en el desarrollo de la bomba atómica. Se valieron de esta invención para la simulación de problemas probabilísticos relacionados con la difusión de neutrones en el material de fisión. La naturaleza aleatoria de la simulación recuerda a una ruleta, razón por la cual debe su nombre al Casino de Montecarlo (Mónaco) por ser “la capital de los juegos de azar”.
¿Qué es la Simulación de Montecarlo?
En términos sencillos, la simulación de Montecarlo implica realizar un gran número de “pruebas” o “escenarios”, donde se va dando diferentes valores a las variables en función de sus respectivas distribuciones de probabilidad. Al final de todas las pruebas, se obtiene una distribución de resultados posibles que permite predecir tendencias o comportamientos.
La premisa bajo la que se desarrolló la herramienta es que la tarea de modelar la variable aleatoria de un experimento aleatorio se hace más sencilla al realizar varias iteraciones del experimento y anotando su resultado, en lugar de tratar de averiguar la función que lo modela teniendo en cuenta las distintas variables que influirán en su resultado.
Aplicación matemática a un activo financiero
Teniendo en cuenta los conceptos aprendidos sobre la distribución normal y su aplicación para generar una fan chart, veamos paso a paso cómo podríamos aplicar la simulación por Montecarlo a un activo financiero basándonos en sus valores históricos. Pero antes es importante mencionar que aplicar la simulación de Montecarlo de esta forma presupone que el comportamiento pasado puede informar sobre el comportamiento futuro. Sin embargo, en el mundo real, hay muchos factores que pueden influir en el precio de un activo, y en esta simulación no se tendrán en cuenta. Por lo tanto, siempre es importante usar esta herramienta como una de varias al lanzar predicciones. Ahora sí, a continuación, se listan los pasos a seguir:
1. Cálculo de Retornos Diarios
A partir de los precios al cierre (EOD, End Of Day) de cada día, calcula los retornos diarios. Estos se obtienen tomando el precio de cierre de un día y dividiéndolo por el precio de cierre del día anterior, y luego restando 1.
r_t = \frac{P_t - P_{t-1}}{P_{t-1}}donde:
- r_t: retorno en el tiempo t
- P_t: precio del activo en el tiempo t
- f(x): precio del activo en el tiempo t-1
2. Estadísticas de los Retornos
Una vez que tengas los retornos diarios, puedes calcular la media \mu y la desviación estándar \sigma de estos retornos. Estos dos parámetros serán cruciales para la simulación.
3. Simulación
Para cada día en el futuro, se genera un retorno aleatorio basado en una distribución normal con la media y desviación estándar calculada anteriormente. Luego, se aplica ese retorno al precio más reciente para obtener el precio simulado del día siguiente. Expresado en una fórmula queda de la siguiente manera:
P_{t+1} = P_t \times (1 + (\mu + \sigma \times Z))donde:
- P_{T+1}: precio del activo en el tiempo t + 1
- \mu: media de los retornos
- \sigma: desviación estándar de los retornos
- Z: número aleatorio proveniente de una distribución normal estándar
4. Múltiples Simulaciones.
La clave de la simulación de Montecarlo es que computa multitud de posibilidades que arrojan una variedad de resultados posibles de un experimento. Si se hacen muchas simulaciones sobre la posible trayectoria que podría seguir el precio del activo, será mas fácil predecir su resultado con la información recolectada, que si lo intentamos predecir en base a todas las variables que podrían influir en él.
5. Resultados:
Al final, tendrás una distribución de precios finales después de un cierto número de días. Esto te permite ver no solo un precio esperado, sino también la variabilidad y los posibles escenarios extremos.
Aplicación a través de código Python
Ahora con la ayuda de Python se llevarán a cabo los pasos anteriores para representar posibles trayectorias que seguirá durante el próximo mes (20 días hábiles futuros) la curva de precios final de día de un hipotético activo financiero.
1) Se simula 4 meses de precios final de día de un activo:
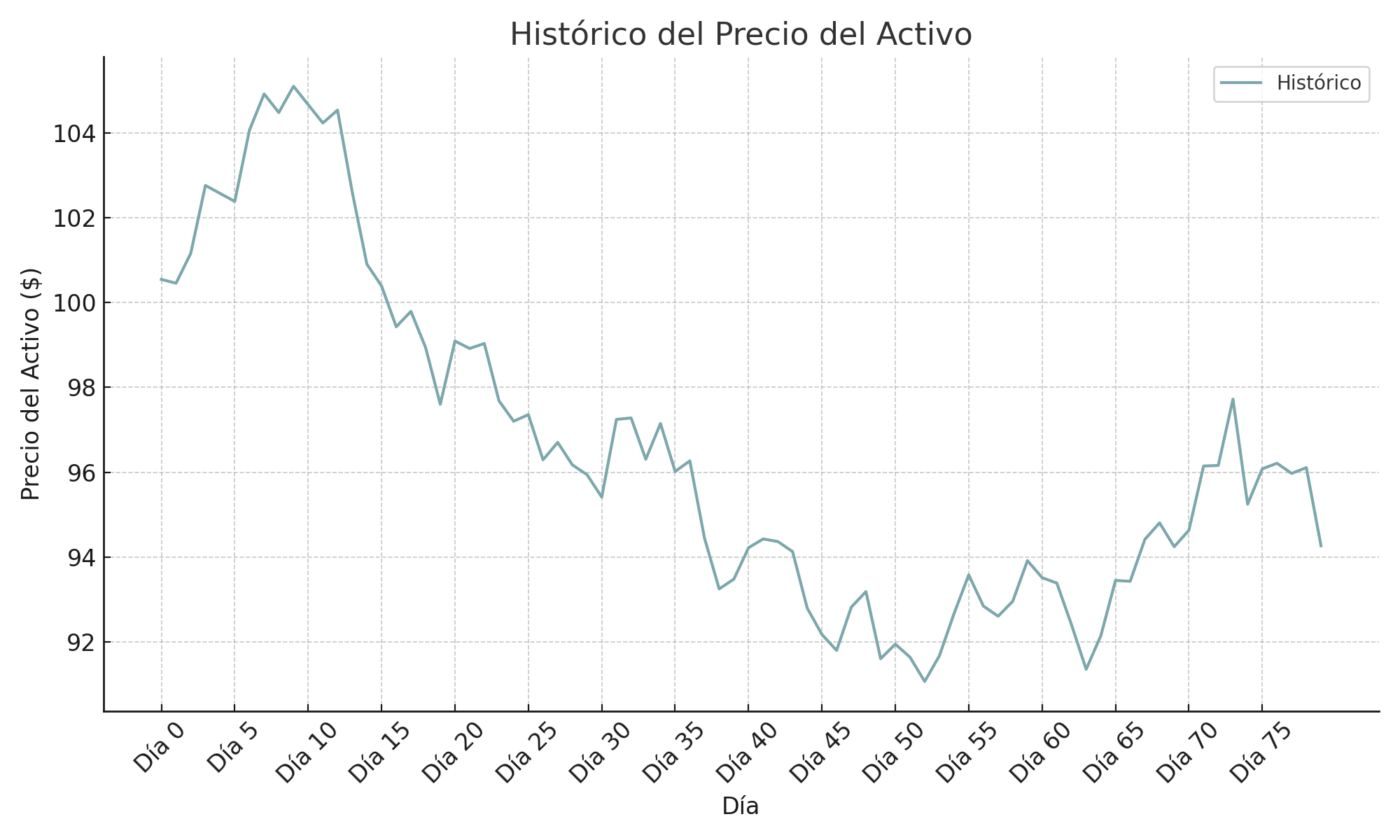
2) Se calcula la media y desviación estándar de los retornos diarios que dan aproximadamente -0.0019 y 0.019 respectivamente.
> Calcular los retornos diarios
retornos = precios.pct_change().dropna()
> Calcular la media y desviación estándar de los retornos
media_retornos = retornos.mean()
desviacion_retornos = retornos.std()
3) Para cada día de predicción, generaremos un retorno aleatorio utilizando la media y desviación estándar calculadas.
retorno_aleatorio = np.random.normal(media_retornos, desviacion_retornos)
4) Usaremos este retorno para calcular el precio del activo para ese día.
Precio_simulado.append(precio_simulado[-1] * (1 + retorno_aleatorio))
5) Se repite este proceso 100 veces para obtener 100 escenarios diferentes de la evolución del precio del activo.
Se grafica el resultado para interpretar de forma intuitiva el resultado de la simulación que elevará la probabilidad de éxito al momento de tomar decisiones:
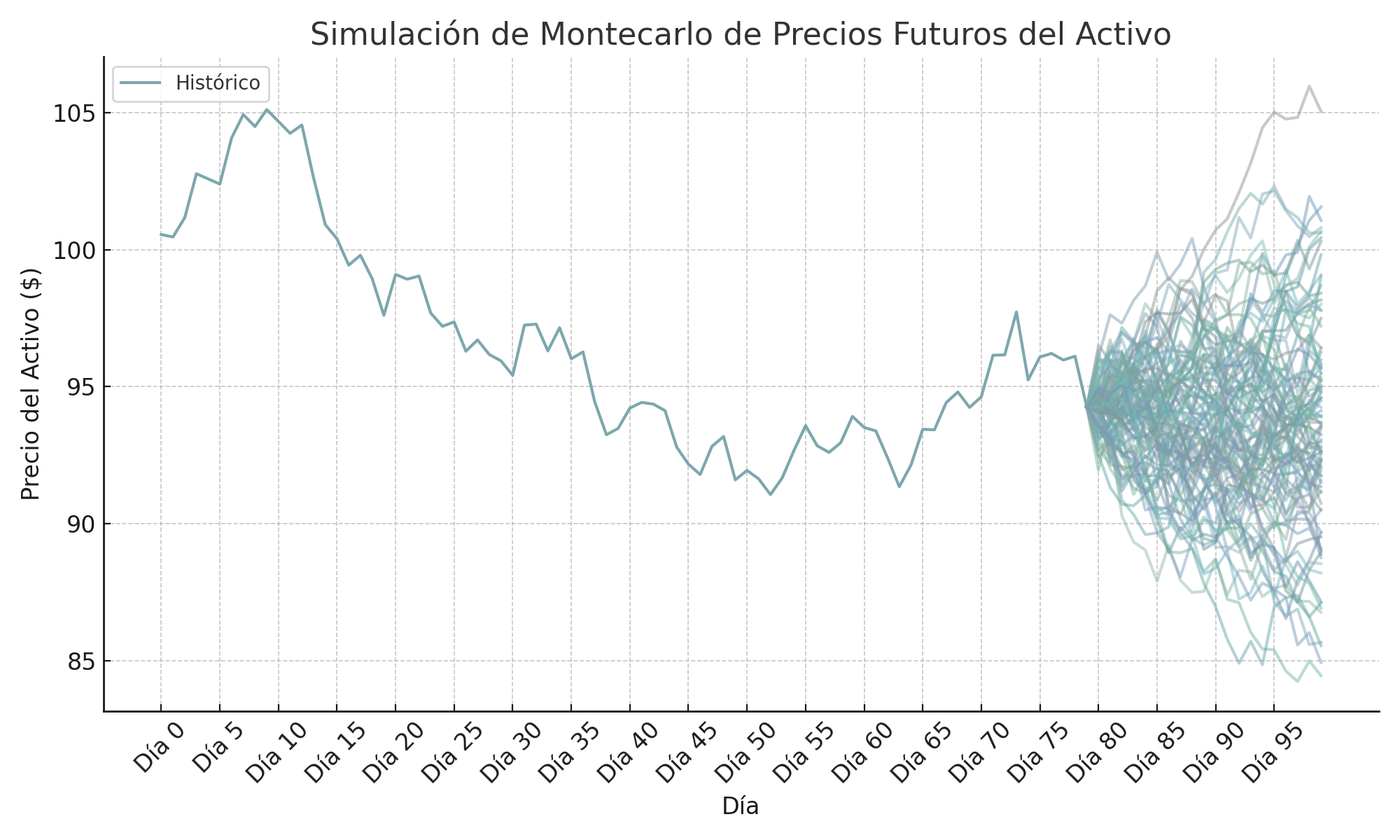
Otras aplicaciones en Finanzas
En el ámbito financiero, la simulación de Montecarlo se utiliza ampliamente para:
- Planificación Financiera: Modelar diferentes escenarios económicos y su impacto en las inversiones o en la planificación de jubilación.
- Precios de Derivados: Calcular el precio de instrumentos financieros complejos que dependen de múltiples factores de riesgo.
- Optimización de Carteras: Entender la relación riesgo-rendimiento de diferentes combinaciones de activos.
- Evaluación de Riesgos: Estimar métricas como el Valor en Riesgo (VaR) para carteras de inversión.
Conclusión
En este artículo se ha expuesto el origen de la Simulación de Montecarlo y en qué consiste a rasgos generales. Después se ha explicado cómo aplicarlo a los datos históricos del precio final de día de un activo financiero a nivel matemático, y después se ha extrapolado a código Python para representar el resultado de la Simulación. Por todo ello, no hay duda de que la Simulación de Montecarlo es una herramienta estadística muy útil para modelar la evolución futura de los activos, ayudando en la toma de decisiones informadas en un mundo financiero complejo y en constante cambio.
En el próximo artículo se tratará el VaR por Montecarlo.
Referencias
Glasserman, P. (2004). Monte Carlo Methods in Financial Engineering (Vol. 53). Springer Science & Business Media.
Benninga, S. (2008). Financial Modeling (3rd ed.). MIT Press.








